Växelspänning #
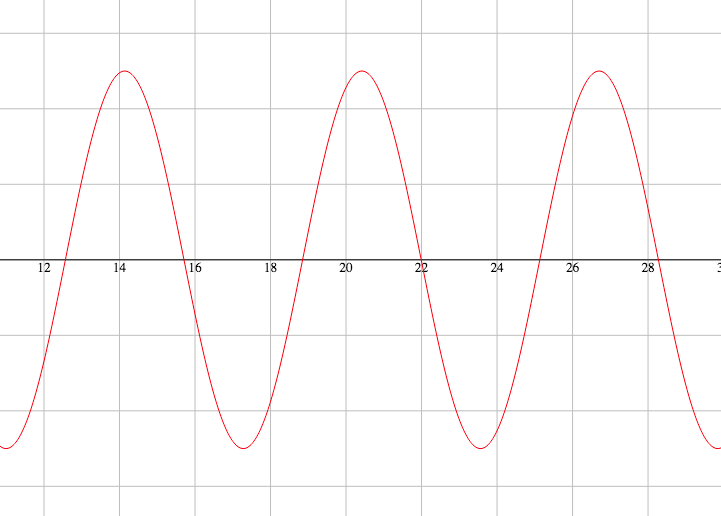
Växelspänning ändrar riktning och storlek hela tiden. Bilden ovanför visar hur spänningen går från 0V till + och sedan tillbaka ner till 0V och till -. Kurvan som syns i bilden heter sinuskurva. Växelspänning har altså inte + och - på samma ställe hela tiden. + och - byter hela tiden platts det kallas att polariteten ändras.
AC #
Ofta kallas växelspänning/växelström för AC vilket betyder Alternating Current.
DC #
Ofta kallas likspänningen/likström (när det finns ett + och ett -) för DC vilket betyder Direct Current.
Toppvärde #
Toppvärdet är det som är högst upp på sinuskurvan.
\( û \)
= Toppvärde
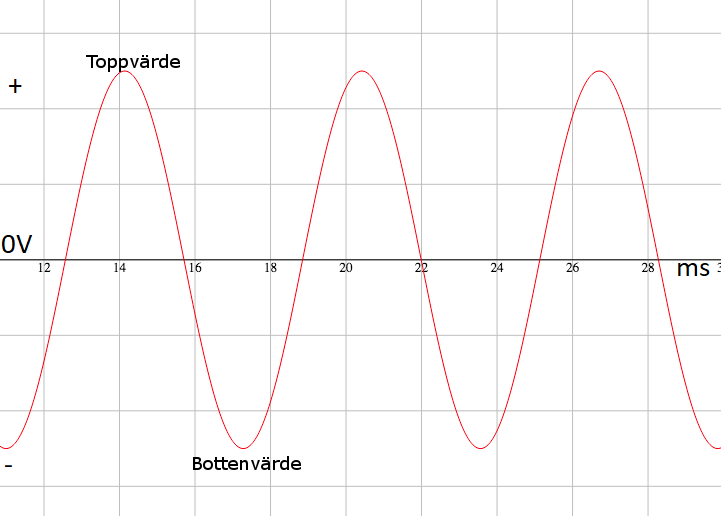
Effektivvärde #
Effektivvärdet är hur stor spänningen är i medel. När polariteten är tvärt om så ändrar det inte riktningen på effektivvärdet. Detta beror på att effektivvärdet beskriver hur stor effekten är inte vilket håll den kommer från. I en DC krets finns bara effektivärdet. Det är effektivvärdet vi använder när vi räknar med tillexmepel Ohms-lag.
\( U \)
= Effektivvärde
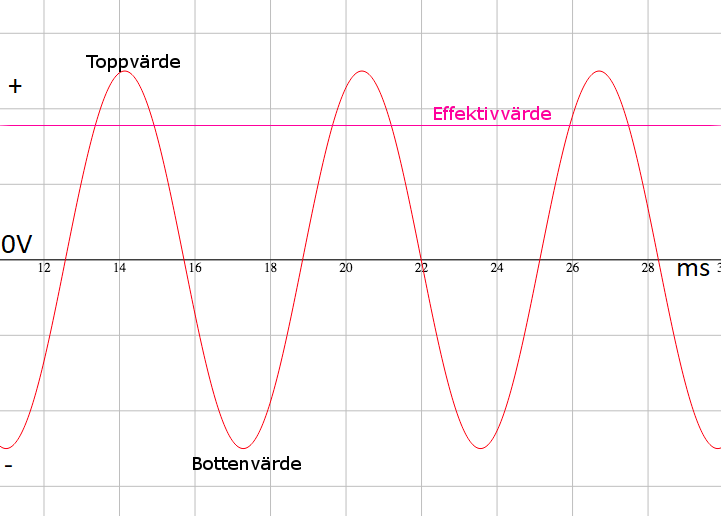
Samband #
Toppvärdet är alltid störren än effektivvärdet eftersom effektivvärdet är medelspänningen för strömmen/spänningen. Effektivvärdet är det samma som spänningen i en DC krets. I en DC krets är toppvärdet och effektivvärdet samma.
Exempel #
Effektivvärdet är alltid lägre än toppvärdet.
Toppvärdet är alltid större än effektivvärdet.
Beräkningar #
För att räkna ut toppvärdet när du har effektivvärdet använder du följande formel.
\( û = U * \sqrt[]{2} \)
Beräkna effektivvärde från toppvärde: #
| Data |
|---|
| \( û = 15V \) |
| Steg | Exempel |
|---|---|
| Formel | \( U = \frac{û}{\sqrt[]{2}} \) |
| Uträkning | \( U = \frac{15V}{\sqrt[]{2}} \) |
| Resultat | \( U = 10.6V \) |
| Svar |
|---|
| \( û = 15V \) |
| \( U = 10.6V \) |
Beräkna toppvärde från effektivvärde: #
| Data |
|---|
| \( U = 230V \) |
| Steg | Exempel |
|---|---|
| Formel | \( û = U * \sqrt[]{2} \) |
| Uträkning | \( û = 230V * \sqrt[]{2} \) |
| Resultat | \( û = 325V \) |
| Svar |
|---|
| \( U = 230V \) |
| \( û = 325V \) |
Periodtid & Frekvens #
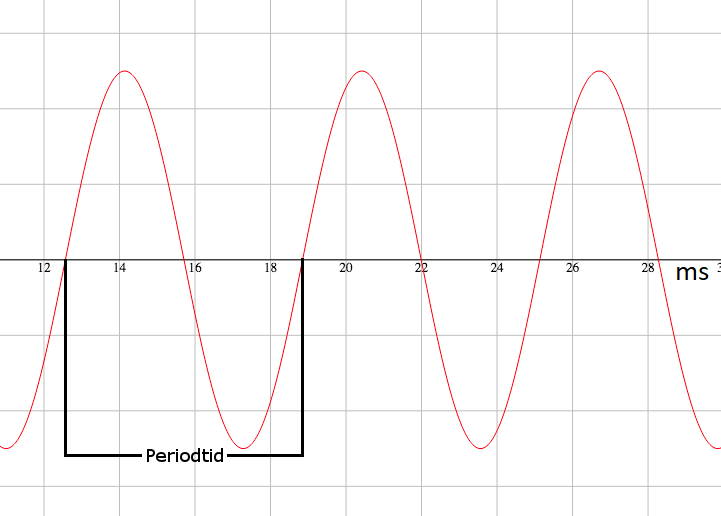
En period växelspänning är från att spänningen börjar öka från 0V och går till sitt max värde, som kallas för toppvärde, till sitt minnsta värde, som kallas för bottenvärde, och upp till 0V igen. Periodtid är hur lång tid det tar för spänningen att gå hela vägen upp ner och upp igen.
Frekvens är hur många gånger något händer per sekund. Det mäts i enheten Hertz(Hz).
Ordet period #
Ordet period är samma som en period är i hockey, innebandy, etc. Alltså en omgång. I boxning heter det rond alltså rund/varv, en elektrisk peroiod är också ett varv för en enkel generator.
Exempel #
Om frekvensen minskar så ökar periodtiden.
Om frekvensen ökar så minskar persiodtiden.
Om periodtiden minskar så ökar frekvensen.
Om periodtiden ökar så minskar frekvensen.
Formel #
För att räkna ut frekvensen så gäller följande formel:
\( f = \frac{1}{t} \)
Beräkna frekvensen från periodtid: #
| Data |
|---|
| \( t = 10ms \) |
| Steg | Exempel |
|---|---|
| Formel | \( f = \frac{1}{t} \) |
| Uträkning | \( f = \frac{1}{0.01s} \) |
| Resultat | \( f = 100Hz \) |
| Svar |
|---|
| \( t = 10ms \) |
| \( f = 100Hz \) |
Beräkna periodtid från frekvensen: #
| Data |
|---|
| \( f = 50Hz \) |
| Steg | Exempel |
|---|---|
| Formel | \( t = \frac{1}{f} \) |
| Uträkning | \( t = \frac{1}{50Hz} \) |
| Resultat | \( f = 0.02s \) |
| Svar |
|---|
| \( f = 50Hz \) |
| \( t = 20ms \) |
Frågor #
Vad är störst av effektivvärde och toppvärde?
Vad är minst av toppvärde och effektivvärde?
Vad händer med frekvensen om periodtiden ökar?
Vad händer med frekvensen om persiodtiden minskar?
Vad händer med periodtiden om frekvensen ökar?
Vad händer med periodtiden om frekvensen minskar?
Storhets och Enhetstabell #
| Storhet | Beteckning | Enhet | Beteckning |
|---|---|---|---|
| Ström (Effektivvärde) | I | Ampere | A |
| Ström (Toppvärde) | î | Ampere | A |
| Spänning (Effektivvärde) | U | Volt | V |
| Spänning (Toppvärde) | û | Volt | V |
| Resistans | R | Ohm | Ω |
| Längd | l | Meter | m |
| Tvärsnittsarea | A | Kvadratmillimeter | mm² |
| Resistivitet | \(\rho\) | Ohm per meter per kvadratmillimeter | Ohm/m/mm² |
| Effekt | P | Watt | W |
| Periodtid | \( t \) | Sekunder | s |
| Frekvens | \( f \) | Hertz | Hz |