Fasförskjutning
#
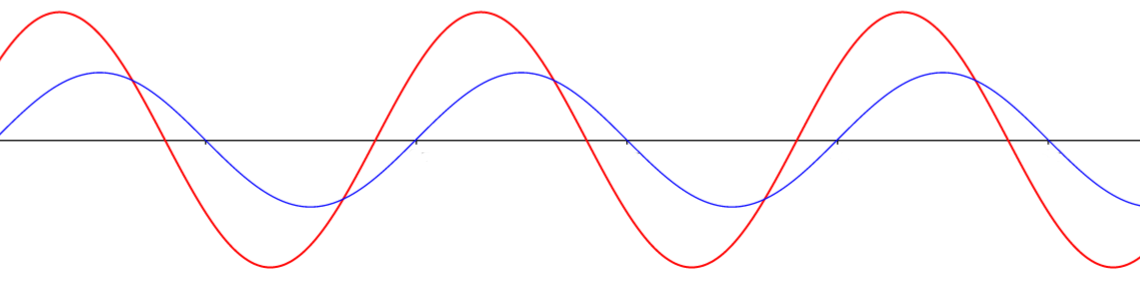
Fasförskjutning är när strömmen och spänningen inte går i takt. Som i bilen ovan så har ström och spänning sina topp och botten värden vid olika tidpunkter. När ström och spänningn inte går i takt så fungerar inte Effekt-formeln och Ohms lag som vanligt längre.
Induktiv
#
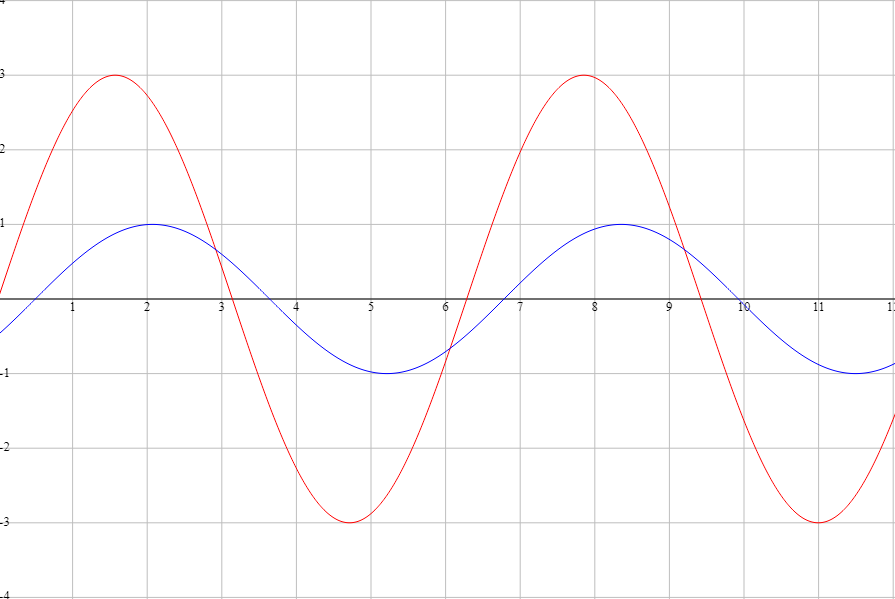
När du kopplar in en spole i en krets kommer strömmen att komma efter spänningen. Det beror på att magnetfältet som skapas i spolen bromsar strömmen. På bilden kan du se hur strömmen (blå) kommer efter spänningen (röd).
Kapasitiv
#
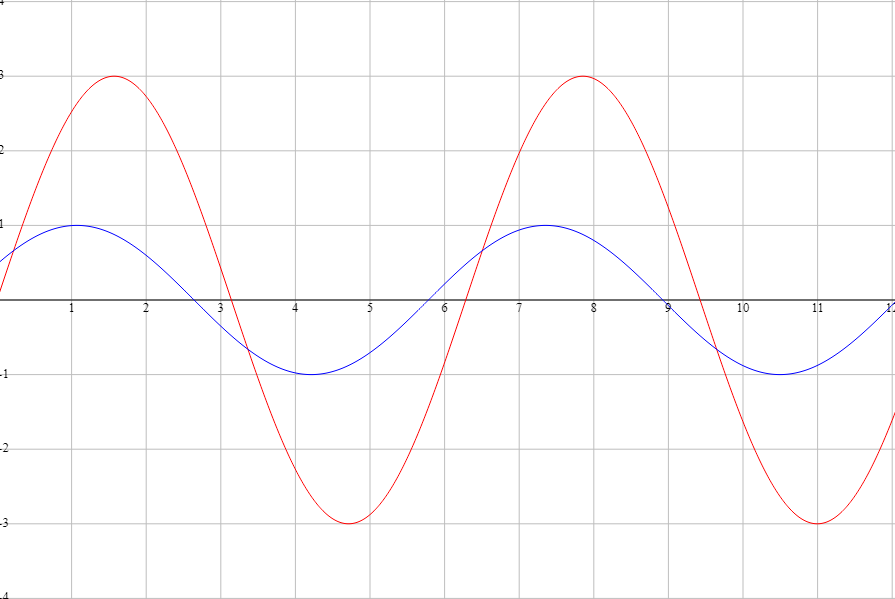
När du kopplar in en kondensatorn i en krets kommer strömmen att komma före spänningen. Det beror på att strömmen tidigare har blivit lagrad i kondensatorn och skickas ut redan innan spänningen kommer. På bilden kan du se hur strömmen (blå) kommer före spänningen (röd).
Ordet fas
#
Ordet effekt används även utanför elvärlden då betyder det nästan samma sak. Ett exempel är att säga att effekten av att slå sig på tummen med hammaren är att man får ont. Om du slår dig jättehårt med hammaren på tummen, får du jätteont, villken är en stor effekt. Om du slår dig lite på tummen, får du lite ont eller liten effekt.
Ordet förskjutning
#
Försjutning betyder att något är flyttat, att något inte ligger tillsammans.
Trianglar
#
När det finns fasförskjutning i en krets, kan du beskriva hur de olika delarna hänger samman med hjälp av trianglar. Grundtrianglarna i en enkel krets med fasförskjutning är dessa:
\(\varphi\)
är samma i alla trianglarna. Vet du vnikeln
\(\varphi\)
i en krets så vet du de andra också, eftersom det är samma.
Faförskjutniung och effekt
#
Skenbar effekt
#
\(S = U * I\)
Effekt
#
\(P = U * I * Cos\varphi\)
Induktiv reaktiv effekt
#
\(Q_l = U * I * Sin\varphi\)
Kapasitiv reaktiv effekt
#
\(Q_c = U * I * Sin\varphi\)
Fasförskjutet motstånd
#
Resistans
#
\(R = Z * Cos\varphi\)
Impedans
#
\(Z = R / Cos\varphi\)
Kapacitiv Reaktans
#
\(Q_c = Z * Sin\varphi\)
Induktiv Reaktans
#
\(Q_l = Z * Sin\varphi\)
Fasförskjutna spänningar
#
Spänning över resistans
#
\(U_r = U * Cos\varphi\)
Huvudspänning
#
\(U = U_r / Cos\varphi\)
Spänning över induktans
#
\(U_l= U * Cos\varphi\)
Spänning över kapasitans
#
\(U_c= U * Cos\varphi\)
Exempel
#
Om en spole är inkopplad i kretsen, kommer strömmen att komma efter spänningen.
Om en kondensator är inkopplad i kretsen, kommer strömmen att komma före spänningen.
Om både en kondensator och en spole är inkopplad i en krets, kommer de att motverka varandra och fasförskjutningen kommer att minska.
Om det är rätt storlek på kondesator och spole, kommer fasförskjutningen att försvinna helt.
Beräkningsexempel fasförskjutning resistans och impedans:
#
Steg
Räkna ut fasförskjutning
Formel
\( Cos\varphi = \frac{R}{Z} \)
Uträkning
\( Cos\varphi = \frac{15Ω}{20Ω} \)
Resultat faktor
\( Cos\varphi = 0.75 \)
Steg
Räkna ut fasförskjutning i grader
Formel
\( \varphi = Cos^{-1}(Cos\varphi) \)
Uträknning
\( \varphi = Cos^{-1}(0.75) \)
Resultat
\( \varphi = 41.4\degree \)
Svar
R = 15Ω
Z = 20Ω
\( Cos\varphi = 0.75 \)
\( \varphi = 41.4\degree \)
Beräkningsexempel fasförskjutning skenbar effekt och effekt:
#
Steg
Räkna ut fasförskjutning
Formel
\( Cos\varphi = \frac{P}{S} \)
Uträkning
\( Cos\varphi = \frac{150W}{200VA} \)
Resultat faktor
\( Cos\varphi = 0.75 \)
Steg
Räkna ut fasförskjutning i grader
Formel
\( \varphi = Cos^{-1}(Cos\varphi) \)
Uträknning
\( \varphi = Cos^{-1}(0.75) \)
Resultat
\( \varphi = 41.4\degree \)
Svar
P = 150W
S = 200VA
\( Cos\varphi = 0.75 \)
\( \varphi = 41.4\degree\)
Beräkningsexempel effekt och skenbar effekt med fasförsjutning:
#
Data
P = 300W
\( Cos\varphi = 0.75 \)
Steg
Räkna ut fasförskjutning
Formel
\( S = \frac{P}{Cos\varphi} \)
Uträkning
\( S = \frac{300W}{0.75} \)
Resultat
\( S = 400VA \)
Svar
P = 150W
\( Cos\varphi = 0.75 \)
S = 400VA
Beräkningsexempel impedans och ström och spänning:
#
Data
\( Z = 300 \Omega\)
\( I = 0.32 A \)
\( U_R = 72 V \)
Steg
Räkna ut Spänningen
Formel
\( U = I * Z \)
Uträkning
\( U = 0.31 A * 300 \Omega \)
Resultat
\( U = 96V \)
Steg
Räkna ut spänningen över reaktiva lasten
Formel
\( U_L^2 = U^2-U_R^2 \)
Uträkning
\( U_L = \sqrt{96V^2-72V^2} \)
Resultat
\( U_L = 63.5V \)
Steg
Räkna ut Skenbara effekten
Formel
\( S = U * I \)
Uträkning
\( S = 96V * 0.32A \)
Resultat
\( S = 30.72 \text{VA} \)
Steg
Räkna ut reaktiva effekten
Formel
\( Q_L = U_L * I \)
Uträkning
\( Q_L = 63.5V * 0.32A \)
Resultat
\( Q_L = 20.32 \text{VAR} \)
Steg
Räkna ut aktiva effekten
Formel
\( P = U_R * I \)
Uträkning
\( P = 72V * 0.32A \)
Resultat
\( P = 23,04W \)
Svar
\( Z = 300 \Omega\)
\( I = 0.32A \)
\( U_R = 72 V \)
\( U = 96VA \)
\( U_L = 63.5V \)
\( S = 30.72 \text{VA} \)
\( Q_L = 20.32 \text{VAR} \)
\( P = 23,04W \)
Frågor
#
Vad händer med strömmen om en spole är inkopplad i en krets?
Vad händer med strömmen om en kondensator är inkopplad i en krets?
Vad händer om du kopplar in både kondensator och en spole i en krets?
Vad händer om du kopplar in en kondensator och en spole med lika stor reaktans?
Storheter och enheter
#
Storhet
Beteckning
Enhet
Beteckning
Ström (Toppvärde)
\(î \)
Ampere
A
Ström (Effektivvärde)
\(I \)
Ampere
A
Spänning (Toppvärde)
\(û\)
Volt
V
Spänning (Effektivvärde)
\(U\)
Volt
V
Spänning över induktiv reaktans
\(U_l\)
Volt
V
Spänning över kapasitiv reaktans
\(U_c\)
Volt
V
Resistans
\(R \)
Ohm
Ω
Kapacitiv reaktans
\(X_c\)
Ohm
Ω
Induktiv reaktans
\(X_l\)
Ohm
Ω
Impedans
\(Z\)
Ohm
Ω
Effekt
\(P\)
Watt
W
Skenbar effekt
\(S\)
VoltAmpere
VA
Reaktiv effekt induktiv
\( Q_l \)
VoltAmpereReaktiv
VAR
Reaktiv effekt kapasitiv
\( Q_c \)
VoltAmpereReaktiv
VAR
Fasförskjutning
\( \varphi \)
Grader
\( \degree \)
Effektfaktor
\( Cos\varphi \)
Faktor
ingen
Verkninsgrad
\( \eta \)
Procent / Faktor
% / ingen
Periodtid
\( t \)
Sekunder
s
Frekvens
\( f \)
Hertz
Hz
Resistivitet
\(\rho\)
Ohm per meter per kvadratmillimeter
Ohm/m/mm²
Längd
\(l \)
Meter
m
Tvärsnittsarea
\(A \)
Kvadratmillimeter
mm²
\(\varphi\)
är samma i alla trianglarna. Vet du vnikeln
\(\varphi\)
i en krets så vet du de andra också, eftersom det är samma.