Parallellkrets #
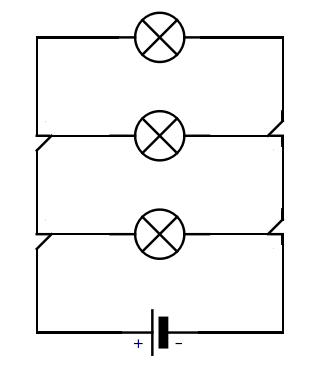
I parallellkretser kopplas komponenterna på varandra, eller parallellt. De kallas också för parallellkopplingar eftersom de kopplas så. I en paralellkrets så får strömmen fler vägar att ta sig fram. Eftersom det finns fler vägar för strömmen så går det mer ström ju fler komponenter som koppas in. Mer ström betyder då att den totala resistansen måste ha blivit mindre.
Den totala resistansen blir alltså mindre än de olika delresistanserna i en parallellkoppling. En bra minnesregel är därför att totalresistansen alltid blir mindre än den minsta resistansen i en parallellkoppling.
Ordet parallell #
För att komma ihåg ordet vad ordet parallell betyder så är det samma ord som du använder i andra lägen så som:
- Parallella universum
- Parallella linjer
- Parallellslalom
Ordet parallell betyder alltså bara att något ligger vid sidan av varandra. Parallella saker korsar inte varandra, när du har dina skidor parallellt så går det bra men korsar du dem så ramlar du direkt.
Samband #
Spänningen #
I en paralellkrets är alla komponeneter direkt kopplade till spänningskällan och har därför samma spänning. Så spänning för komponent 1,2 och 3 har samma spänning i en parallellkrets. \(U = U_1 = U_2 = U_3...\)
Strömmen #
I en parallellkrets så finns det flera olika strömmar eftersom strömmen kan ta flera olika vägar. Strömmen som kommer från spänningskällan är så summan av alla strömmarna. \(I = I_1 + 1_2 + I_3...\)
Resistansen #
I en parallellkrets så minskar resistasen ju fler komponenter som kopplas in. Detta beror på att att strömmen får flera vägar att gå. Eftersom strömmen har flera vägar att gå så kommer den totala strömmen att öka utan att spänningen ändras. Då säger Ohms lag att resistansen har minskat. Alltså fler komponenter innebär lägre resistans. Det finns olika sätt att räkna ut resistansen antingen genom att räkna ut den totala strömmen och räkna ut resistansen med hjälp av Ohms lag eller genom att använda någon av dessa formler:
Basform #
\(\frac{1}{R_{tot}} = \frac{1}{R_1} + \frac{1}{R_1} + \frac{1}{R_3} + ...\)Beräkningsform #
\(R_{tot} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_1} + \frac{1}{R_3} + ...}\)Bråkform #
\(R_{tot} = \frac{R_1*R_2}{R_1+R_2}\)
Denna fungerar bara på två parallellkopplade motstånd.
Exempel #
Om du lägger till en resistor i en parallellkrets så minskar resistansen eftersom strömmen får fler vägar att gå.
Om du tar bort en resistor i en parallellkrets så ökar resistansen eftersom strömmen får färre väggar att gå.
Om du lägger till eller tar bort en resistor i en parallellkrets så påverkas inte spänningen i kretsen.
Om du lägger till en resistor i en parallellkrets så ökar strömmen eftersom det finns fler vägar för den att gå genom kretsen.
Om du tar bort en resistor i en parallellkrets så minskar strömmen eftersom det finns färre vägar för strömmen att röra sig genom kretsen.
Beräkningar #
Beräkningsexempel för resistans #
| Data |
|---|
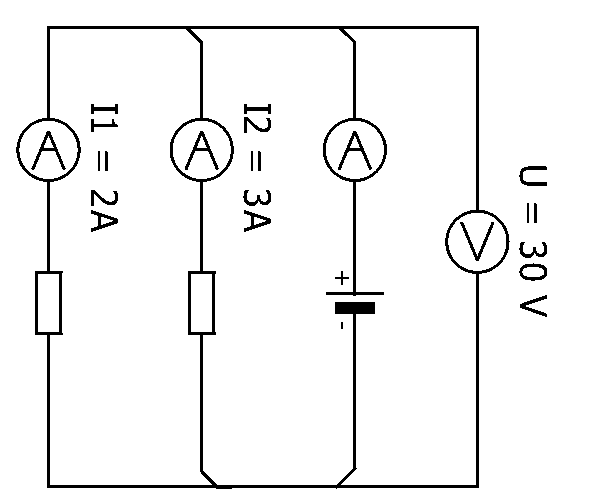
| \( U = 30 V \) |
| \( I_1 = 2 A \) |
| \( I_2 = 3 A \) |
| Steg | Uträkning av totala strömmen |
|---|---|
| Formel | \( I = I_1+I_2 \) |
| Uträkning | \( I = 2 A + 3 A \) |
| Resultat | \( I = 5 A \) |
| Steg | Uträkning av totala resistansen allternativ 1 |
|---|---|
| Formel | \( R_{tot} = \frac{U}{I} \) |
| Uträkning | \( R_{tot} = \frac{ 30 V }{ 5 A } \) |
| Resultat | \( R_{tot} = 6 \Omega \) |
| Steg | Uträkning av resistans 1 |
|---|---|
| Formel | \( R_1 = \frac{U}{I_1} \) |
| Uträkning | \( R_1 = \frac{ 30 V }{ 2 A } \) |
| Resultat | \( R_1 = 15 \Omega \) |
| Steg | Uträkning av resistans 2 |
|---|---|
| Formel | \( R_{tot} = \frac{U}{I_2} \) |
| Uträkning | \( R_{tot} = \frac{ 30 V }{ 3 A } \) |
| Resultat | \( R_{tot} = 10 \Omega \) |
| Steg | Uträkning av totala resistansen allternativ 2 |
|---|---|
| Formel | \( \frac{1}{R_{tot}} = \frac{1}{R_1} + \frac{1}{R_2} \) |
| Uträkning | \( \frac{1}{R_{tot}} = \frac{1}{ 15 \Omega } + \frac{1}{ 10 \Omega } \) |
| Uträkning | \( R_{tot} = \frac{1}{ 0.833333} \) |
| Resultat | \( R_{tot} = 6 \Omega \) |
| Svar |
|---|
| \( U = 30 V \) |
| \( I_1 = 2 A \) |
| \( I_2 = 3 A \) |
| \( I = 5 A \) |
| \( R_{tot} = 6 \Omega \) |
| \( R_1 = 15 \Omega \) |
| \( R_{tot} = 10 \Omega \) |
| \( R_{tot} = 6 \Omega \) |
Beräkningsexempel för spänning och ström: #
| Data |
|---|
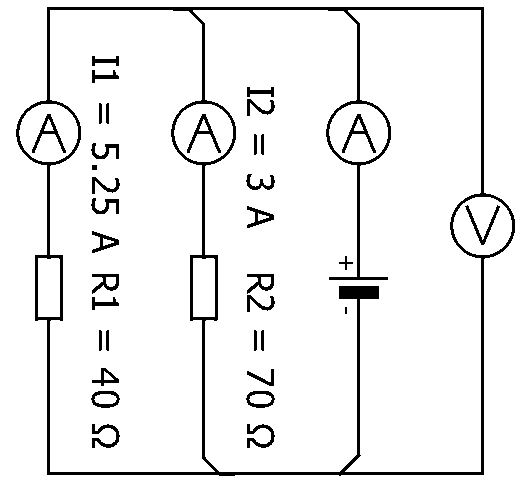
| \( I_1 = 5.25 A \) |
| \( I_2 = 3 A \) |
| \( R_1 = 40 \Omega \) |
| \( R_2 = 70 \Omega \) |
| Steg | Uträkning av totala strömmen |
|---|---|
| Formel | \( I = I_1+I_2 \) |
| Uträkning | \( I = 5.25 A + 3 A \) |
| Resultat | \( I = 8.25 A \) |
| Steg | Uträkning av spänning alternativ 1 |
|---|---|
| Formel | \( U = I_1 * R_1 \) |
| Uträkning | \( U = 5.25 A * 40 \Omega \) |
| Resultat | \( U = 210 V \) |
| Steg | Uträkning av spänning alternativ 2 |
|---|---|
| Formel | \( U = I_1 * R_1 \) |
| Uträkning | \( U = 3 A * 70 \Omega \) |
| Resultat | \( U = 210 V \) |
| Steg | Uträkning av totala resistansen allternativ 1 |
|---|---|
| Formel | \( R_{tot} = \frac{U}{I} \) |
| Uträkning | \( R_{tot} = \frac{ 210 V }{ 8,25 A } \) |
| Resultat | \( R_{tot} = 25.5 \Omega \) |
| Steg | Uträkning av totala resistansen allternativ 2 |
|---|---|
| Formel | \( \frac{1}{R_{tot}} = \frac{1}{R_1} + \frac{1}{R_2} \) |
| Uträkning | \( \frac{1}{R_{tot}} = \frac{1}{ 40 \Omega } + \frac{1}{ 70 \Omega } \) |
| Uträkning | \( R_{tot} = \frac{1}{ 0.0392857} \) |
| Resultat | \( R_{tot} = 25.5 \Omega \) |
| Svar |
|---|
| \( I_1 = 5.25 A \) |
| \( I_2 = 3 A \) |
| \( R_1 = 40 \Omega \) |
| \( R_2 = 70 \Omega \) |
| \( R_{tot} = 25.5 \Omega \) |
| \( U = 210 V \) |
| \( I = 8.25 A \) |
Frågor #
Vad händer om du lägger till en resistor i en parallellkrets?
Vad händer om du tar bort en resistor i en parallellkrets?
Vad händer med spänningen över resistorerna i en parallellkrets om du lägger till en resistor?
Vad händer med spänningen över resistorerna i en parallellkrets om du tar bort en resistor?
Vad händer med strömmen i en parallellkrets om du lägger till en resistor?
Vad händer med strömmen i en parallellkrets om du tar bort en resisor?