Seriekrets #
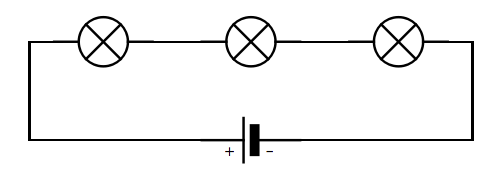
I seriekretsar kopplar man komponenter i serie eller efter varandra, ungefär som ett tåg. Detta kallas också för seriekopplingar. Det som händer i seriekopplingen är att strömmen får svårare att ta sig fram, efter som det är fler motstånd att ta sig förbi, och då minskar strömmen. Spänningen kommer däremot dela upp sig på varje del i seriekopplingen. Hur stor spänningen över komponent blir beror på hur stor resistorn är och hur stor strömmen är, för att räkna ut det avänder man Ohms-Lag.
Ordet serie #
Ordet serie i detta fall är samma princip som när man använder order i vanliga fall också så som:
- Seriemördare
- Serietidning
- Seriespel Serie betyder alltså att något sker i en följd efter varandra. En seriemördare mördar en sedan nästa osv, till skillnad från tillexempel en massmördare som mördar många samtidigt.
Samband #
Spänningen #
Spänningn från spänningskällan kommer att delas upp över de olika belastningar. Alla spänningarna över belastningarna kommer tillsammans bli den spänning som spänningskällan ger. \(U = U_1+U_2+U_3...\)
Strömmen #
I en seriekrets finns det bara en väg för strömmen att gå. Därför finns det bara en ström i kretsen. Strömman är alltså lika stor över allt i kretsen.
\(I = I_1 = 1_2 = I_3...\)
Resistansen #
Eftersom strömmen måste gå igenom alla belastningar den ena efter den andra blir detn totala resistansen summan av alla belastningarnas resistans.
\(R_{tot} = R_1+R_2+R_3...\)
Exempel #
Om du lägger till en belastning i serie så kommer den totala resistansen att öka eftersom strömmen får ytterligare ett hinder att passera.
Om du tar bort en belastning som sitter i serie och kopplar ihop så att strömmen kan passera direkt minskar resistansen eftersom strömmen slipper går igenom den belastningen.
Om du lägger till en belastning i serie så sjunker spänningen över dom andra belastningarna i seriekretsen.
Om du har två resistorer i serie och en har stor resistans och en har liten så kommer den med stor resistans få en hög spänning och den med låg resistans kommer att få en låg spänning. Detta beror på att båda kommer att få samma ström och strömmen gånger resistansen ger spänningen enligt Ohms-lag. Detta gör att spänningen blir hög med hög resistans och låg med låg resistans.
Beräkningar #
Beräkningsexempel för spänning: #
| Data |
|---|
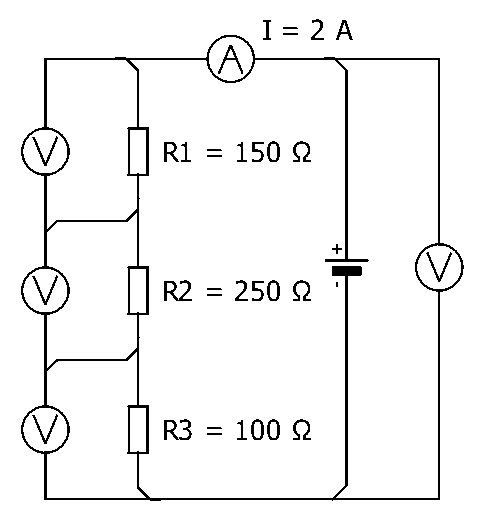
| \( I = 2 A \) |
| \( R_1 = 150 \Omega \) |
| \( R_2 = 250 \Omega \) |
| \( R_3 = 100 \Omega \) |
| Steg | Uträkning av totala resistansen |
|---|---|
| Formel | \( R_{tot} = R_1+R_2+R_3 \) |
| Uträkning | \( R_{tot} = 150 \Omega + 250 \Omega + 100 \Omega \) |
| Resultat | \( R_{tot} = 500 \Omega \) |
| Steg | Uträkning av delsspänningen 1 |
|---|---|
| Formel | \( U_1 = R_1 * I \) |
| Uträkning | \( U_1 = 150 \Omega * 2 A\) |
| Resultat | \( U_1 = 300 V \) |
| Steg | Uträkning av delsspänningen 2 |
|---|---|
| Formel | \( U_2 = R_2 * I \) |
| Uträkning | \( U_2 = 250 \Omega * 2 A\) |
| Resultat | \( U_2 = 500 V \) |
| Steg | Uträkning av delsspänningen 3 |
|---|---|
| Formel | \( U_3 = R_3 * I \) |
| Uträkning | \( U_3 = 100 \Omega * 2 A\) |
| Resultat | \( U_3 = 200 V \) |
| Steg | Uträkning av totala spänningen, alternativ 1 |
|---|---|
| Formel | \( U = R_{tot} * I \) |
| Uträkning | \( U = 500 \Omega * 2 A\) |
| Resultat | \( U = 1000 V \) |
| Steg | Uträkning av totala spänningen, alternativ 2 |
|---|---|
| Formel | \( U = U_1+U_2+U_3\) |
| Uträkning | \( U = 300 V + 500 V + 200 V \) |
| Resultat | \( U = 1000 V \) |
| Svar |
|---|
| \( I = 2 A \) |
| \( R_1 = 150 \Omega \) |
| \( R_2 = 250 \Omega \) |
| \( R_3 = 100 \Omega \) |
| \( R_{tot} = 500 \Omega \) |
| \( U_1 = 300 V \) |
| \( U_2 = 500 V \) |
| \( U_3 = 200 V \) |
| \( U = 1000 V \) |
Beräkningsexempel för resistans och ström: #
| Data |
|---|
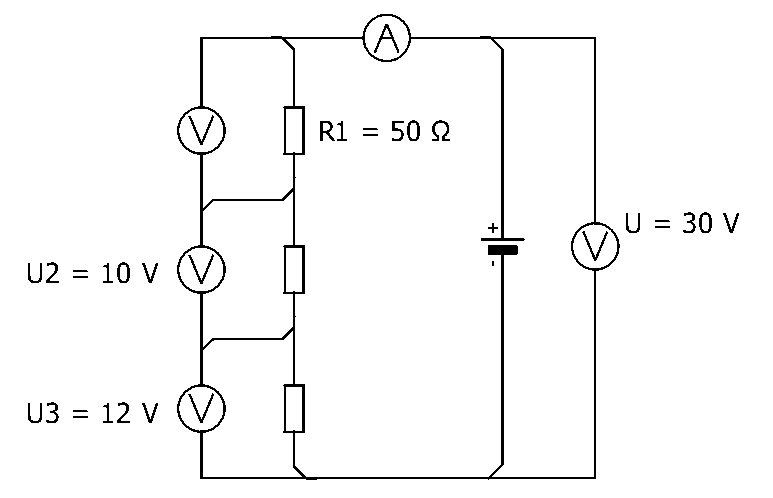
| \( U = 30 V \) |
| \( R_1 = 50 \Omega \) |
| \( U_2 = 10 V \) |
| \( U_3 = 12 V \) |
| Steg | Uträkning av delspänning 1 |
|---|---|
| Formel | \( U_1 = U - (U_2 + U_3) \) |
| Uträkning | \( U_1 = 30V - (10V + 12V) \) |
| Resultat | \( U_1 = 8V \) |
| Steg | Uträkning av strömmen |
|---|---|
| Formel | \( I = \frac{U_1}{R_1}\) |
| Uträkning | \( I = \frac{8V}{50 \Omega}\) |
| Resultat | \( I = 0.16A \) |
| Steg | Uträkning av resitansen 2 |
|---|---|
| Formel | \( R_2 = \frac{U_2}{I}\) |
| Uträkning | \( R_2 = \frac{10V}{0.16A}\) |
| Resultat | \( R_2 = 62.5 \Omega \) |
| Steg | Uträkning av resitansen 3 |
|---|---|
| Formel | \( R_3 = \frac{U_3}{I}\) |
| Uträkning | \( R_3 = \frac{12V}{0.16A}\) |
| Resultat | \( R_3 = 75 \Omega \) |
| Steg | Uträkning av totala resistansen, alternativ 1 |
|---|---|
| Formel | \( R_{tot} = \frac{U}{I} \) |
| Uträkning | \( R_{tot} = \frac{30V}{0.16A}\) |
| Resultat | \( R_{tot} = 187,5 \Omega\) |
| Steg | Uträkning av totala resistansen, alternativ 2 |
|---|---|
| Formel | \( R_{tot} = R_1 + R_2 + R_3 \) |
| Uträkning | \( R_{tot} = 50 \Omega + 62.4 \Omega + 75 \Omega \) |
| Resultat | \( R_{tot} = 187,5 \Omega\) |
| Svar |
|---|
| \( U = 30 V \) |
| \( R_1 = 50 \Omega \) |
| \( U_2 = 10 V \) |
| \( U_3 = 12 V \) |
| \( U_1 = 8V \) |
| \( I = 0.16A \) |
| \( R_2 = 62.5 \Omega \) |
| \( R_3 = 75 \Omega \) |
| \( R_{tot} = 187,5 \Omega\) |
Frågor #
Vad händer om du lägger till till en resistor i en seriekrets?
Vad händer om du tar bort en resistor i en seriekrets?
Vad händer med spänningen över resistorerna i en seriekrets om du lägger till en resistor?
Vad händer med spänningen över resistorerna i en seriekrets om du tar bort en resistor?
Vad händer med strömmen i en seriekrets om du lägger till en resistor?
Vad händer med strömmen i en seriekrets om du tar bort en resistor?